OpenCilk concepts
OpenCilk programming is a bit of a departure from traditional serial programming, and requires a somewhat different "world scale" in order to write OpenCilk programs that perform and scale well. In this section, we will introduce and explain some concepts that are fundamental to OpenCilk programming, and indeed, important for any parallel programmer to understand. First, we will introduce a way to describe the structure of a OpenCilk program as a graph of strands and knots. Next, we will discuss how to analyze the expected performance of an OpenCilk program in terms of work, span, and parallelism.
Strands and knots
Traditional serial programs are often described using call graphs or class hierarchies. Parallel programming adds another layer on top of the serial analysis. In order to diagram, understand and analyze the parallel performance of an OpenCilk program, we will distinguish only between sections of code that run serially, and sections that may run in parallel.
We will use the word strand to describe a serial section of the program. More precisely, we define a strand as "any sequence of instructions without any parallel control structures."
Note that according to this definition, a serial program could be made up of many sequential strands as short as a single instruction each, a single strand consisting of the entire program, or any other partitioning. We will assume that sequential strands are always combined to make a single, longer strand.
In addition, we will define a knot as the point at which three or more strands meet. An OpenCilk program will have two kinds of knots - a spawn knot and a sync knot. Here's a picture illustrating 4 strands (1, 2, 3, 4), a spawn knot (A) and a sync knot (B).
Here, only strands (2) and (3) may execute in parallel.
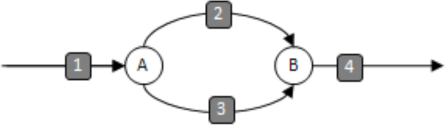
A Cilk++ program fragment that has this structure is:
do_stuff_1(); // execute strand 1
cilk_spawn func_3(); // spawn strand 3 at knot A
do_stuff_2(); // execute strand 2
cilk_sync; // sync at knot B
do_stuff_4(); // execute strand 4
In these illustrations, the strands are represented by lines and arcs, while the knots are represented by the circular nodes. We will refer to a strand/knot diagram as a Directed Acyclic Graph (DAG) that represents the serial/parallel structure of an OpenCilk program.
Note: In some published literature (including some papers about Cilk and Cilk++), you will see similar diagrams in which the work is done in the nodes rather than the arcs.
In a Cilk++ program, a spawn knot has exactly one input strand and two output strands. A sync knot has two or more input strands and exactly one output strand. Here is a DAG with two spawns (labeled A and B) and one sync (labeled C). In this program, the strands labeled (2) and (3) may execute in parallel, while strands (3), (4), and (5) may execute in parallel.
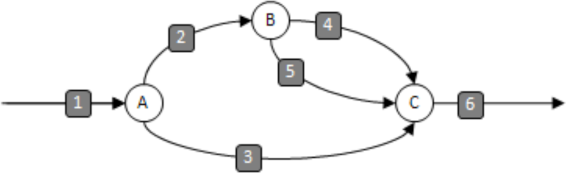
A DAG represents the serial/parallel structure of the execution of an OpenCilk program. With different input, the same OpenCilk program may have a different DAG. For example, a spawn may execute conditionally. However, the DAG does NOT depend on the number of processors on which the program runs, and in fact the DAG can be determined by running the OpenCilk program on a single processor. Later, we will describe the execution model, and explain how work is divided among the number of available processors.
Work and span
Now that we have a way of describing the serial/parallel structure of an OpenCilk program, we can begin to analyze the performance and scalability. Consider a more complex OpenCilk program, represented in the following diagram.
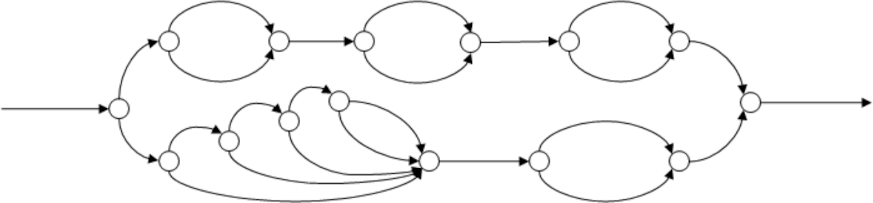
This DAG represents the parallel structure of some Cilk++ program. The ambitious reader might like to try to construct a OpenCilk program that has this DAG.
Let's add labels to the strands to indicate the number of milliseconds it takes to execute each strand:
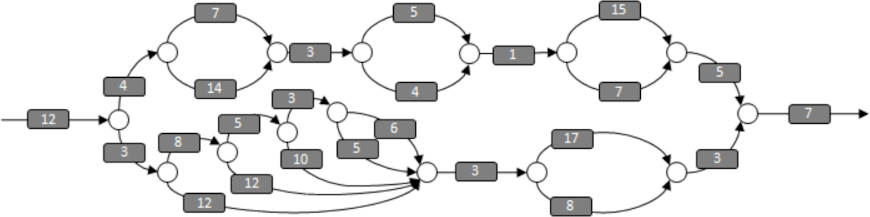
Work
The total amount of processor time required to complete the program is the sum of all these numbers. We call this the work.
In this DAG, the work is 181 milliseconds for the 25 strands shown, and if the program is run on a single processor, the program should run for 181 milliseconds.
Span
Another useful concept is the span, sometimes called the critical path length. The span is the most expensive path that goes from the beginning to the end of the program. In this DAG, the span is 68 milliseconds, as shown below:
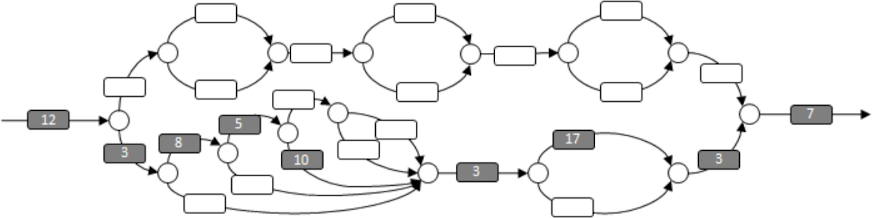
In ideal circumstances (e.g., if there is no scheduling overhead) then, if an unlimited number of processors are available, this program should run for 68 milliseconds.
With these definitions, we can use the work and span to predict how an OpenCilk program will speedup and scale on multiple processors. The math is fairly simple, but we'll change the names a bit to confuse you.
When analyzing a OpenCilk program, we like to talk about the running time of the program on various numbers of processors. We'll use
is the Work is the Span
Note that on 2 processors, the execution time can never be less than
Similarly, for P processors, the execution time is never less than the execution time on an infinite number of processorrs, hence the Span Law:
Speedup and parallelism
Intuitively, if a program runs twice as fast on 2 processors, then the speedup is 2. We formalize this by defining the speedup on P processors as:
The maximum possible speedup would occur using an infinite number of processors. Thus, we define the parallelism as:
Estimating performance and scalability
So what good is all this? Well, if we had some way to measure Cilkscale does. Measuring the work
For the rest of us, Cilkscale reports the parallelism by combining its knowledge of the DAG with measurements of the time spent executing each strand. Using these and other measurements, Cilkscale provides a speedup estimate and other information that provides valuable insights into the behavior of an OpenCilk program.